Рекурсивная блочная схема вычисления присоединенной и обратной матриц.
Для QT-формата был реализован рекурсивный алгоритм вычисления присоединенной и обратной матриц, а также решения систем линейных уравнений (см. [13] и [14]).
Вычисления производились с плотной случайной целочисленной матрицей 128 порядка, с 28-битовыми целыми коэффициентами. Была составлена программа с помощью рекурсивного алгоритма [14] для QT-формата.
Этот алгоритм вычисления присоединенной матрицы в коммутативной области имеет такую же сложность, что и алгоритма матричного умножения, который в нем используется. Для построения параллельного алгоритма был применен последовательный алгоритм вычисления присоединенной матрицы, в котором все процедуры умножения выполнялись параллельно. Результаты экспериментов приведены на рис 7. Коэффициент ускорения при переходе с двух на 14 процессоров равен 60%.
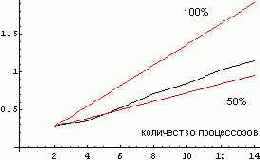
Рис. 7. Вычисление присоединенной (обратной) матрицы в случае целых коэффициентов в QT формате с помощью рекурсивного алгоритма. Коэффициент ускорения равен 60%.
